Suma de Riemann

Las sumas de Riemann se utilizan para hacer una aproximación del área limitada por una curva y el eje de abscisas.

Si y=f(x)$y=f(x)$ es una función continua en el intervalo [a,b]$[a,b]$, y definimos un conjunto finito de puntos a=x0<x1<…<xn=b$a=x_0<x_1<\dots <x_n=b$, se define la suma inferior de Riemann como:

                                                           

sn=∑i=1nmi(xi−xi−1),

donde mi$m_i$ es el valor más bajo que toma la función en el intervalo [xi,xi−1]$[x_i,x_{i-1}]$. Se define también la suma superior de Riemann como:

Sn=∑i=1nMi(xi−xi−1),

donde Mi$M_i$ es el valor más alto que toma la función en el intervalo [xi,xi−1]$[x_i,x_{i-1}]$.

El gráfico interactivo permite visualizar ambas sumas de rectángulos para distintos valores de n$n$.

Ejemplo:

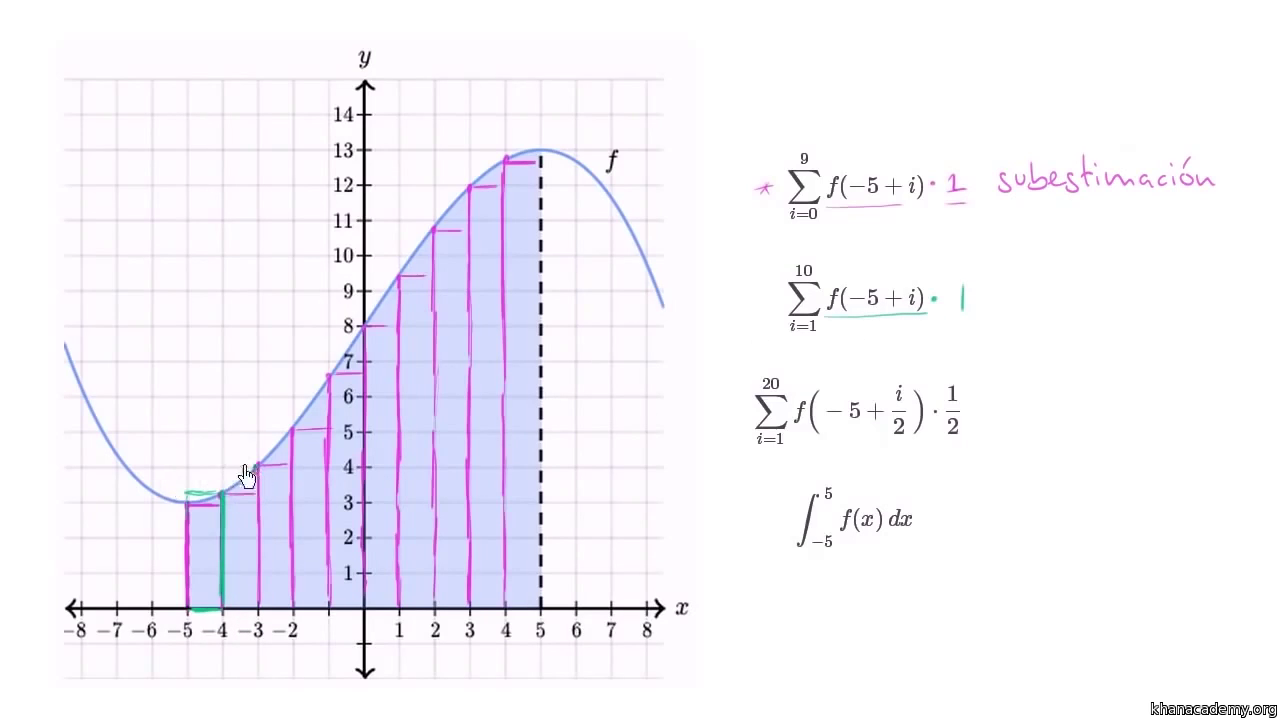
Cuanto mayor sea el número de rectángulos, las dos sumas se van aproximando al área bajo la curva, de manera que en el límite tenemos.

                                           limn→∞sn=limn→∞Sn.

A este valor del área al que tienden las dos sumas lo llamamos integral definida entre a y b, representándola como:

                                                       ∫baf(x)dx,

y como queda dicho, es el área encerrada entre la gráfica de la función y=f(x)$y=f(x)$, el eje de abscisas y las rectas x=a$x=a$ y x=b$x=b$.

Calculo Integral de 2periodo

Ejemplos: Aqui se mostraran unos ejemplos de ejercicios ya hechos de integrales.

Estas son las siguientes tipos de integradas estas utilizan las formulas de la 10 a la 20 seria un nuevo tema en lo que se veria en un segundo periodo de Bachillerato o Preparatoria.