Calculo Integral
lunes, 19 de noviembre de 2018
Solucion de integrales indefinidas
Primer Metodo :
Una integral que contiene una expresiones cuadratica de tres terminos ax2 + bx + c o de dos terminos ax2 + bx, puede reducirse a otra con expreciones de alguna v2 -+ a2 o a2 - v2 completando un trinomio cuadrado perfecto ( sustitucion algebraica) que se representa por TCP.
Segundo Metodo : Cuando el integrado es una fraccion cuyo numerador es una expresion de primer grado y el denominador de segundo grado o raiz de ella,la integral puede reducirse a una integral inmediata,tal y como se explica a continuacion.
sábado, 17 de noviembre de 2018
Integral Definida
La integral definida es un concepto utilizado para determinar el valor de las áreas limitadas por curvas y rectas. Dado el intervalo [a, b] en el que, para cada uno de sus puntos x, se define una función f (x) que es mayor o igual que 0 en [a, b], se llama integral definida de la función entre los puntos a y b al área de la porción del plano que está limitada por la función, el eje horizontal OX y las rectas verticales de ecuaciones x = a y x = b.
Procedimiento:
a) Se obtiene la integral indefinida
b) Se sustituye el limite superior en la variable de la integral indefinida.
c) Se sustituye el limete inferior en la variable de la integral definida.
d) Al valor obtenido en el inaso ´b´ le restamos el valor obtenido en el inciso ´c´ para obtener asi la integral definida.
Ejemplos:
1:

2:






miércoles, 24 de octubre de 2018
Suma de Riemann
Las sumas de Riemann se utilizan para hacer una aproximación del área limitada por una curva y el eje de abscisas.
Si y=f(x) es una función continua en el intervalo [a,b] , y definimos un conjunto finito de puntos a=x0<x1<…<xn=b , se define la suma inferior de Riemann como:
sn=∑i=1nmi(xi−xi−1),
donde mi es el valor más bajo que toma la función en el intervalo [xi,xi−1] . Se define también la suma superior de Riemann como:
Sn=∑i=1nMi(xi−xi−1),
donde Mi es el valor más alto que toma la función en el intervalo [xi,xi−1] .
El gráfico interactivo permite visualizar ambas sumas de rectángulos para distintos valores de n .
Ejemplo:
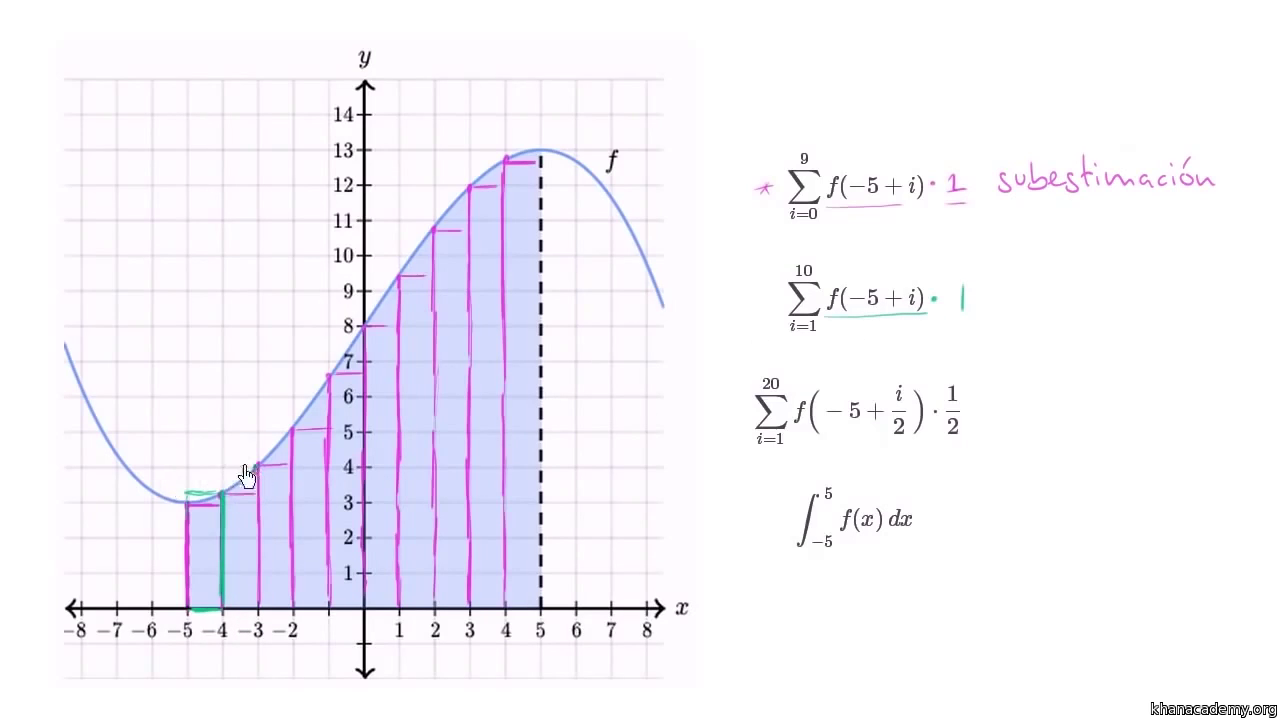
Cuanto mayor sea el número de rectángulos, las dos sumas se van aproximando al área bajo la curva, de manera que en el límite tenemos.
limn→∞sn=limn→∞Sn.
A este valor del área al que tienden las dos sumas lo llamamos integral definida entre a y b, representándola como:
∫baf(x)dx,
y como queda dicho, es el área encerrada entre la gráfica de la función y=f(x) , el eje de abscisas y las rectas x=a y x=b .
Calculo Integral de 2periodo
Ejemplos: Aqui se mostraran unos ejemplos de ejercicios ya hechos de integrales.
Estas son las siguientes tipos de integradas estas utilizan las formulas de la 10 a la 20 seria un nuevo tema en lo que se veria en un segundo periodo de Bachillerato o Preparatoria.
miércoles, 19 de septiembre de 2018
Aplicar Formulas
Aplicar Formulas
Cuando el integrando está formado por un producto (o una división, que podemos tratar como un producto) se recomienda utilizar el método de integración por partes que consiste en aplicar la siguiente fórmula:
Cuando el integrando está formado por un producto (o una división, que podemos tratar como un producto) se recomienda utilizar el método de integración por partes que consiste en aplicar la siguiente fórmula:
Regla mnemotécnica: Un Día Vi Una Vaca MENOS Flaca Vestida De Uniforme (UDV = UV - FVDU).
Aunque se trata de un método simple, hay que aplicarlo correctamente.
Método:
El integrando debe ser un producto de dos factores.
Uno de los factores será u y el otro será dv.
Se calcula du derivando u y se calcula v integrando dv.
Se aplica la fórmula.
Escoger adecuadamente u y dv:
Una mala elección puede complicar más el integrando.
Supongamos que tenemos un producto en el que uno de sus factores es un monomio (por ejemplo x3). Si consideramos dv = x3. Entonces, integrando tendremos que v = x4/4, con lo que hemos aumentado el grado del exponente y esto suele suponer un paso atrás.
Normalmente, se escogen los monomios como u para reducir su exponente al derivarlos. Cuando el exponente es 0, el monomio es igual a 1 y el integrando es más fácil.
Algo parecido ocurre con las fracciones (como 1/x). Si consideramos dv = 1/x, tendremos v = log|x| y, probablemente, obtendremos una integral más difícil.
Ejemplo:
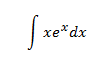
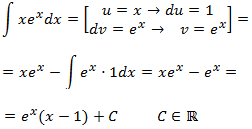
Resolver la Integral
Resolver una Integral:
La integración constituye la operación inversa a la derivación. Suele decirse que, si bien la derivación es una ciencia, la integración es un arte. Esto se debe simplemente a que esta última es más difícil, ya que las derivadas solo tienen relación con el comportamiento de una función en un punto, mientras que, para las integrales, dado que son sumas glorificadas, es necesario tener un conocimiento global de la función.
1 Considera el monomio x n
2
Lleva a cabo la regla de potencias para las integrales. Esta constituye la misma regla de potencias que para las derivadas excepto a la inversa. La potencia se incrementa por 1 y dividimos entre esta nueva potencia. Recuerda añadir la constante de integración C.
3
Aplica la linealidad. La integración es una operación lineal. Esto quiere decir que la integral de una suma es igual a la suma de las integrales y se puede excluir el coeficiente de cada término de la siguiente forma:
4
Encuentra la antiderivada de la función f(x)= x4+2x3 - 5x2 - 1. Este es un polinomio. Por tanto, puedes calcular con facilidad la antiderivada si empleas la propiedad de linealidad y la regla de potencias.
5
Encuentra la antiderivada de la función . Si bien esta podría parecer una función que desafíe nuestras reglas, al observarla, notarás que la fracción puede separarse en tres fracciones y se puede encontrar la antiderivada aplicando la linealidad y la regla de potencias.
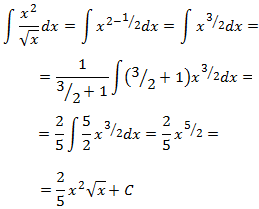
Suscribirse a:
Comentarios (Atom)