Resolver una Integral:
La integración constituye la operación inversa a la derivación. Suele decirse que, si bien la derivación es una ciencia, la integración es un arte. Esto se debe simplemente a que esta última es más difícil, ya que las derivadas solo tienen relación con el comportamiento de una función en un punto, mientras que, para las integrales, dado que son sumas glorificadas, es necesario tener un conocimiento global de la función.
1 Considera el monomio x n
2
Lleva a cabo la regla de potencias para las integrales. Esta constituye la misma regla de potencias que para las derivadas excepto a la inversa. La potencia se incrementa por 1 y dividimos entre esta nueva potencia. Recuerda añadir la constante de integración C.
3
Aplica la linealidad. La integración es una operación lineal. Esto quiere decir que la integral de una suma es igual a la suma de las integrales y se puede excluir el coeficiente de cada término de la siguiente forma:
4
Encuentra la antiderivada de la función f(x)= x4+2x3 - 5x2 - 1. Este es un polinomio. Por tanto, puedes calcular con facilidad la antiderivada si empleas la propiedad de linealidad y la regla de potencias.
5
Encuentra la antiderivada de la función . Si bien esta podría parecer una función que desafíe nuestras reglas, al observarla, notarás que la fracción puede separarse en tres fracciones y se puede encontrar la antiderivada aplicando la linealidad y la regla de potencias.
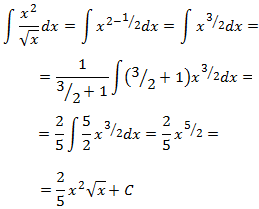
No hay comentarios:
Publicar un comentario