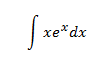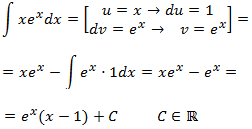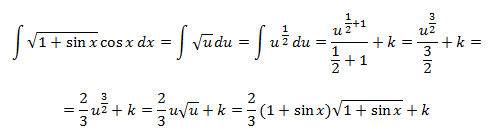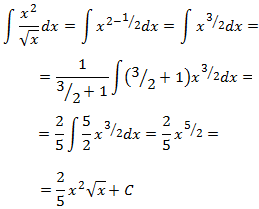Aplicar Formulas

                                                 Aplicar Formulas

Cuando el integrando está formado por un producto (o una división, que podemos tratar como un producto) se recomienda utilizar el método de integración por partes que consiste en aplicar la siguiente fórmula:


                                           

Regla mnemotécnica: Un Día Vi Una Vaca MENOS Flaca Vestida De Uniforme (UDV = UV - FVDU).

Aunque se trata de un método simple, hay que aplicarlo correctamente.

Método:

El integrando debe ser un producto de dos factores.

Uno de los factores será u y el otro será dv.

Se calcula du derivando u y se calcula v integrando dv.

Se aplica la fórmula.

Escoger adecuadamente u y dv:

Una mala elección puede complicar más el integrando.

Supongamos que tenemos un producto en el que uno de sus factores es un monomio (por ejemplo x³). Si consideramos dv = x³. Entonces, integrando tendremos que v = x⁴/4, con lo que hemos aumentado el grado del exponente y esto suele suponer un paso atrás.

Normalmente, se escogen los monomios como u para reducir su exponente al derivarlos. Cuando el exponente es 0, el monomio es igual a 1 y el integrando es más fácil.

Algo parecido ocurre con las fracciones (como 1/x). Si consideramos dv = 1/x, tendremos v = log|x| y, probablemente, obtendremos una integral más difícil.

Ejemplo:

                                              

Resolver la Integral

Resolver una Integral:


La integración constituye la operación inversa a la derivación. Suele decirse que, si bien la derivación es una ciencia, la integración es un arte. Esto se debe simplemente a que esta última es más difícil, ya que las derivadas solo tienen relación con el comportamiento de una función en un punto, mientras que, para las integrales, dado que son sumas glorificadas, es necesario tener un conocimiento global de la función.

1 Considera el monomio  x n

2

Lleva a cabo la regla de potencias para las integrales. Esta constituye la misma regla de potencias que para las derivadas excepto a la inversa. La potencia se incrementa por 1 y dividimos entre esta nueva potencia. Recuerda añadir la constante de integración C.

3

Aplica la linealidad. La integración es una operación lineal. Esto quiere decir que la integral de una suma es igual a la suma de las integrales y se puede excluir el coeficiente de cada término de la siguiente forma:

4

Encuentra la antiderivada de la función f(x)= x4+2x3 - 5x2 - 1. Este es un polinomio. Por tanto, puedes calcular con facilidad la antiderivada si empleas la propiedad de linealidad y la regla de potencias.

5

Encuentra la antiderivada de la función ${\displaystyle f(x)={\frac {2x^{2}+3x-1}{x^{1/3}}}}$. Si bien esta podría parecer una función que desafíe nuestras reglas, al observarla, notarás que la fracción puede separarse en tres fracciones y se puede encontrar la antiderivada aplicando la linealidad y la regla de potencias.

Integrales Indefinidas

                                   Integrales Indefinidas

En cálculo infinitesimal, la función primitiva o antiderivada de una función f es una función F cuya derivada es f, es decir, F ′ = f.

Una condición suficiente para que una función f admita primitivas sobre un intervalo es que sea continua en dicho intervalo.

Si una función f admite una primitiva sobre un intervalo, admite una infinidad, que difieren entre sí en una constante: si F₁ y F₂ son dos primitivas de f, entonces existe un número real C, tal que F₁ = F₂ + C. A C se le conoce como constante de integración. Como consecuencia, si F es una primitiva de una función f, el conjunto de sus primitivas es F + C. A dicho conjunto se le llama integral indefinidade f y se representa como.

Calculo Diferencial

                                              Calculo Integral

Consiste en calcular, en general,superficies curvilineas es decir,el area entre la grafica de una funcion y el eje - x
Si (x) es una funcion positiva en el intevalo a,b
entonces el area que encierra esta funcion y el eje x, dentro del intervalo -a,b es igual 
A=S  dx